Apr 18 2012

introducing OpenLayers Symbology

a JavaScript library for thematic mapping in OpenLayers

At last October’s NACIS Practical Cartography Day I gave a very sweaty presentation that was later described as bewildering and incoherent.  I had always meant to partially redeem myself by packaging and cleaning up the code that formed the basis of that talk.  And here it is!

OL-Symbology is just a small JavaScript library for easily creating 5 basic thematic map types dynamically in OpenLayers: choropleth, proportional symbol, cartogram, dot density, and isoline. Each basic symbology includes many options for customization, and symbology classes can be combined to create multivariate thematic layers. Below I’ll go through the background and specific features of the library; if you just want to check out the code, head over to the Github page for the project.

Impetus

OpenLayers has been around for six years now, and really is the most fully-featured web mapping platform going. I’d argue that it’s been used mostly for reference mapping, as opposed to thematic data mapping. I first saw OL used for thematic mapping in choropleth and proportional symbol applications in 2008. I added noncontiguous cartograms to the mix last year.

These previous implementations, though, were all written and presented more or less as “one offs”. That is, they weren’t packaged up as classes to be re-used by other developers; rather they were all more proofs of concept. I wanted to expand and develop a library of classes that would allow end developers or cartographers to easily create basic thematic mapping types with very little code. Before getting into the library, I need to mention the one previous attempt I know of to do pretty much the same thing: the MapFish widgets for choropleth and proportional symbol mapping.

MapFish is a RIA framework for web mapping that uses OpenLayers as its map engine. I saw the two MapFish thematic mapping widgets mentioned in the 2008 post by Bjørn Sandvik on choropleth mapping with GeoJSON, and I’m really not sure that any work has been done on them since then. Though the MapFish widgets are quite limited — only one color scheme for choropleth, no classed choropleth or unclassed proportional symbols, only one shape type available for proportional symbols — I did borrow some ideas from the format and organization of the two widgets. Before talking about the five individual thematic mapping types in my library, I’ll just go through a bit of what they hold in common.

Common features

To create a new thematic layer, the user/developer only needs to set three options:

  1. url or layer: a data source, in the form of a URL string or a pre-loaded Vector Layer
  2. indicator or valuator: the name of the variable (attribute/indicator) that you are representing with this symbology. If you need to standardize your variable (ex. disease cases divided by population) just define the optional valuator function
  3. map: the Map instance that the thematic layer should be added to

All other symbology settings are optional and have at least semi-intelligent defaults. So, most basically:

var isoLayer = new ol.thematic.Isoline( map, {
   url   : 'geothermal.geo.json',
   indicator    : 'temp_depth_75km'
});

That would create a completely serviceable isarithmic representation and add it to your map, though you’d likely want to customize it by at least setting the isoline interval option (the default is 5; see below).

Each thematic map type has unique options (colorScheme for choropleth, maxSize for proportional symbols, etc.); but they share a few classification options: classed, numClasses, classification method, and classBreaks. The classification method is currently limited to quantiles or equal interval, though any breaks can be applied by setting the classBreaks option. Below I’ll just touch on the 5 thematic map types and the symbology options that can be applied to each.

Symbologies

Choropleth

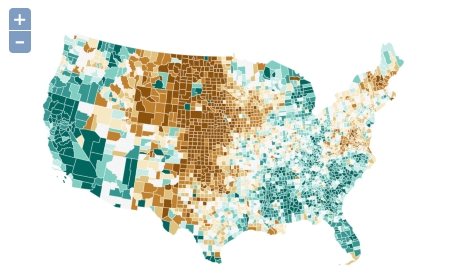
OL-Symbology choropleth

Choropleth is one of the most basic thematic mapping types, and was the first I programmed for this library. To add a choropleth layer to your map, the only required options are the indicator and url:

var choroLayer = new ol.thematic.Choropleth( map, {
   url   : 'counties.json',
   indicator    : 'unemployment'
});

To create a more custom representation, the class includes many different symbology options:

choroLayer = new ol.thematic.Choropleth( map, {
    url         : 'counties.json',
    indicator   : 'unemployment',
    classed  : true,
    numClasses  : 6,
    method   : ol.thematic.Distribution.CLASSIFY_BY_QUANTILE,
    colorScheme : 'GnBu'
});

The color scheme “GnBu” is the name of a ColorBrewer color scheme. All of the ColorBrewer schemes are available just by referencing their reference name. Alternatively users can set the colors property to any custom colors they’d like.

One property not shown above is the colorStrokes boolean. If set to true, feature strokes will also be colored. While this can be applied to polygonal features in a traditional choropleth map, it is perhaps most useful in applying a choropleth symbology to isolines or other linear features (see “multivariate symbologies” below).

Here’s an advanced example that shows most of the options available in the Choropleth class.

Proportional Symbol

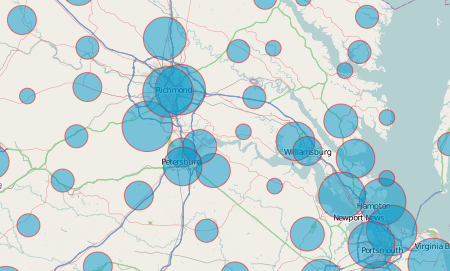
OL-Symbology proportional symbols

Proportional symbols are another basic representation of a quantitative dataset, and can be created just as simply as choropleth layers (above). As with all other symbologies, proportional symbols may be classed (graduated) or unclassed. Symbols themselves can be circles, squares, or triangles; the correct area will be applied no matter what shape is chosen. Similar to the colorStrokes property of the Choropleth class, the ProportionalSymbol class includes a sizeStrokes option that allows feature strokes to be sized instead of feature areas. This property is most useful in multivariate applications (for example, sizing the strokes of isolines to represent the value of each isarithm).

A unique feature of this library is that it allows for perceptual scaling of proportional symbol features. Back in they heyday of psychophysical research in academic cartography, a lot of studies showed that map readers routinely underestimated the size of areal symbols. To correct for this, symbols can be scaled up by an exponent derived from a power function designed to estimate the relationship between actual and perceived size of symbols. For academics and other researchers interested in tweaking the power function exponent, this can be set with the powerFunctionExponent option (the default is the .8747 average derived from James Flannery’s touchstone 1971 study). Most users should just ignore perceptual scaling and use the mathematical default.

Perceptual scaling and other options are shown off in this advanced example of the ProportionalSymbol class.

Noncontiguous Cartogram

OL-Symbology noncontiguous cartogram

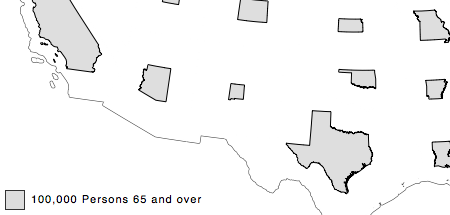
I’m kind of a fan of noncontiguous cartograms — I’ve written about them here, here, and here. My noncontiguous cartogram class just extends the ProportionalSymbol class, so all options (besides shape; see above) for prop symbols are also available for cartograms (classification, perceptual scaling, etc.).

To see the Cartogram class in action, check out this example. And as before, I created a reproduction of the iconic noncontiguous cartogram from Judy Olson’s touchstone study of the form.

Dot Density

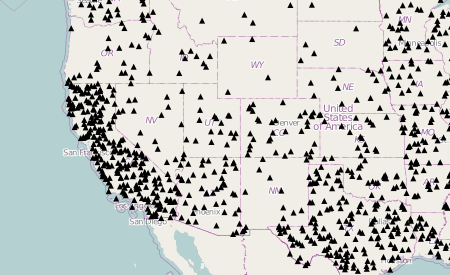
OL-Symbology dot density

Another basic textbook thematic symbology is dot density, in which dots are randomly scattered across polygons in numbers according to their indicator value. The dotValue option controls the ratio of dots to indicator units, and thus the number of dots on the map. The dot size (as well as dot shape) can be set on the defaultSymbolizer object — a style object that each symbology class has that controls non-data related styling properties of the representation. View the source of this example for more.

You may notice that the dot density representation takes a while to process. The basic strategy for creating a dot density layer is to figure out how many dots need to be placed for each polygonal feature, and then to place those dots randomly within the bounds of the features. To accomplish this goal, dots are randomly placed within the bounding box of each feature and then tested to see if they actually lie within the feature. Though this requires some processing, it doesn’t need to be as slow as the current implementation in this library. It is slow only because I decided to use the built-in containsPoint method of the OpenLayers Polygon geometry class. This point-in-polygon method requires that random points be tested one-at-a-time; a much faster strategy (the one Andy and I used when developing this symbology for Indiemapper) is to use a points-in-polygon test that can test many points at a time. Eventually I’ll implement that method here but for now this class should work plenty fast with a small number of features and relatively high dotValue.

Isolines

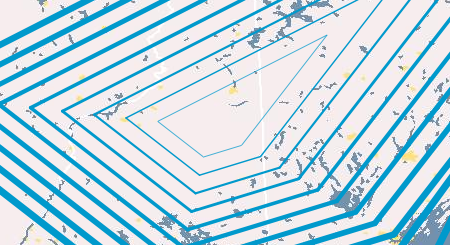
OL-Symbology weighted isolines

Making your browser interpolate isolines is fun! I first did these in ActionScript 3 back in 2008. This JavaScript version works essentially the same way: generating a triangulated irregular network (TIN), interpolating isoline interval values along each triangle edge, and then connecting these interpolated points to form lines of constant value (isolines). See my older post for more description of the basic method. Check out this simple example of the OL-Symbology Isoline class.

The only options available to customize your isoline representation are interval (the distance in attribute space between lines) and showTIN (whether to show the triangulated irregular network used to interpolate the isolines). As described in the next section, you can also apply choropleth and proportional symbologies to your isolines after creation.

Multivariate symbologies

These thematic mapping classes were written in such a way that they can be easily combined to form bivariate and trivariate representations. Of course, this only makes sense with certain symbology combinations; and map readers are bad enough at interpreting univariate symbologies that increased complexity should rarely be attempted. But for those rare cases, OL-Symbology can be used like so:

var choropleth;
var cartogram = new ol.thematic.Cartogram( map, {
    url         : url,
    indicator   : indicator,
    requestSuccess   : function( request )
    {
        choropleth = new ol.thematic.Choropleth( map, {
            indicator : otherIndicator,
            layer : this.layer
        });
    }
});

That would create a noncontiguous cartogram and then color the features with a choropleth color scheme, accepting all defaults; see the example. There are a few things to note in the above. The requestSuccess method can be defined on any symbology object — it is called only once, when remote features have been loaded and processed. The choropleth class is instantiated in the above without a url option — that is because the features have already been loaded from the remote URL. Instead of defining the URL the layer option is set to the layer property of the cartogram representation. Interestingly, the exact same representation would be created by reversing the order and first creating a choropleth representation, and then sizing the features using a cartogram representation.

The same strategy was used to create the image at the top of this post of colored isolines. You can see a basic colored isolines example here. Other possible symbology combinations include proportional symbol + choropleth, dot density + choropleth, isolines + proportional symbols, and proportional symbol + proportional symbol (where the 2nd instance of the ProportionalSymbol class would apply to the proportional symbols’ strokes).

Limitations and next steps

When I presented this work last October, I also showed off a very similar library I’d written that works with Polymaps instead of OpenLayers. Those classes still need some work, and I’ll blog about them separately. The OpenLayers version I’m presenting here is really pretty full-featured, including basic and advanced options for all symbologies. This version is limited to OpenLayers, but the dependencies aren’t that deep so most of the code could be modified to work with another JavaScript mapping API.

Most classes are decently fast, with dot density being the only one I’d hesitate to use in production; but I’ll add my own point-in-polygon method to the dot density class soon. I hope the library is useful to at least a few others, either in pedagogical or production contexts. And it’s BSD licensed so do whatever you want with it!

Tagged , , , , , , , , , , , , , , , | Comments (12) |
Oct 18 2011

Hexbins!

Binning is a general term for grouping a dataset of N values into less than N discrete groups. These groups/bins may be spatial, temporal, or otherwise attribute-based. In this post I’m only talking about spatial (long-lat) and 2-dimensional attribute-based (scatterplot) bins. Such binnings may be thought of as 2D histograms. This may make more or less sense after what lies beneath.

If you’re just after that sweet honey that is my code, bear down on my Github repository for this project — hexbin-js.

Rectangular binning

The simplest 2D bin is rectangular. Indeed, for most purposes rectangular bins suffice, and their computational simplicity is a significant advantage.

The above is a shot from a little example I produced on jsFiddle, while learning Mike Bostock’s fantastic D3 JavaScript library for HTML and SVG data-binding and visualization. The example demonstrates the need for and the technique of 2D rectangular binning and aggregation.

Binning can be good for both the users and the creators/developers of static or interactive thematic maps or other visualizations. For the user, showing every single point can lead to cognitive overload, and may even be inaccurate, as overlapping points lead to a misreading of density.

In the above image (from Antaeus Concepts) the data points are represented in black, and due to overlap the true concentration/density distribution is indiscernible from the graphic.

A binned representation may reveal patterns not readily seen in the raw point representation of the data (see Antaeus’ sunflower plot for the same data below). For the developer or cartographer, too, binning can present an advantage, chiefly in efficiency. Back in the day, manual cartographers probably weren’t too keen on drawing 10’s of 1000’s of data points — I’m guessing they’d rather do the cheap bin math so that they could then only draw 10’s or 100’s of uniformly-shaped bins to represent the same data.

Though we modern cartographers have fancy-fangled computers to draw our data points for us, even these beasts hiccup when asked to draw 10,000+ points at once. Hiccups are acceptable in static rendering, but not in real-time apps that employ animation (as even at just 5 frames per second, rendering 1000s of points each frame would prove intensive for even newer home desktops).

So anyway, binned representations can be beneficial for both users and creators. Below I’ll just describe one binning method (hexagon binning, or hexbinning), its implementation, and some examples.

Hexagonal binning

I first encountered hexagonal binning in the sweet 2006 O’Reilly book by Joseph Adler, Baseball Hacks. Adler demonstrates the need for binning by showing a “spraychart” of David Ortiz’s 2003 balls-in-play.

Adler writes,

Clearly, you can see that David Ortiz tends to hit balls more often to right field. Wouldn’t it be nice to have a cleaner way to see this density? We’ll use another visualization technique, called hexagonal binning, to get a clearer picture of where Ortiz’s hits land.

The idea of hexagonal binning is to break a two-dimensional plane into different bins. First, the bins make interlocking hexagons. It is possible to use squares (or interlocking triangles or another shape), but hexagons look “rounder” than squares.

To turn his spraychart into hexbins, Adler used the hexbin package for R developed by Nicholas Lewin-Koh and Martin Maechler (inspired by Dan Carr’s work; more on this below).

Though unfortunately printed smaller in the book than the spraychart, I think the hexbin representation does effectively simplify the data while revealing patterns not easily retrieved from the full spraychart representation.

Hex history and theory

The technique of using interlocking hexagons to aggregate 2-dimensional data was first described in a 1987 paper by four Pacific Northwest Laboratory statisticians (D.B. Carr et al, “Scatterplot Matrix Techniques for Large N”). The authors note, though, that they were inspired by another binning technique — sunflower plots — described a few years earlier by William Cleveland and Robert McGill.

Cleveland and McGill (1984, “The Many Faces of a Scatterplot”) didn’t mention hexagons; indeed they specified that squares be used to bin the data, with each bin then being tranformed into a “sunflower”, with each “petal” representing a datum within the bin:

In their later 1987 paper, D.B. Carr et al suggested that hexagon-bin-based sunflowers represented the data more faithfully than the rectangular-bin version. They cite various reasons for this advantage, but I think it basically comes down to Joseph Adler’s later observation that “hexagons look rounder than squares”. Indeed, a regular tessellation of a 2D surface is not possible with polygons of greater than six sides, making the hexagonal tessellation the most efficient and compact division of 2D data space.

Besides hexbin sunflower plots, D.B. Carr et al note two other possible symbologies to employ once the data have been successfully hex-binned. To use thematic mapping parlance, the methods are proportional symbols and choropleth. These symbologies and other possibilities are discussed below.

Hexbin symbologies

Hexbinning consists of 1) laying a hexagonal grid or lattice atop a 2-dimensional field of data and 2) determining data point counts for each hexagon. This says nothing of the symbolization or representation method that can then be employed to communicate these counts to the graphic’s reader.

Sunflower plots

Sunflowers are likely the most complex symbology for representing hexbins, but I’m covering them first in this section because they actually inspired the hexbinning method itself.

The above screenshot is from the Antaeus statistics project, and hexagonal sunflower plots have also been implemented within the popular Stata statistics package:

Whether square-bin or hexbin-based, these sunflower plots are notable for allowing the user to simultaneously view generalities and retrieve specifics. A higher number of “petals” leads to a darker hexagon, and clusters of such hexagons will reveal the overall trend of the data. At the same time, individual petals can be counted to determine the exact number of data lying within each hexagonal bin.

Proportional symbol

The choropleth and proportional symbologies don’t really need any explanation here, so images should suffice.

Choropleth
Multivariate

In a multivariate hexbin representation, the secondary variable can be anything, though the sum or average of some attribute of the binned points within each hex would be typical.

In the below, a bivariate symbology is shown, though in this case the variable distribution represented by color value/saturation is the same as that represented by size (making this a redundant symbolization).

In addition to size and saturation/value, alpha (opacity) could also be used to represent a hex attribute (see the bottom of this example page for a value-by-alpha representation of density above a Google map).

Implementation

As noted above, hexbins have been implemented in a few statistical packages, including R. But I haven’t seen any other implementations, and certainly not a client-side one. At first I tried to just port the R code, but it made no sense to me, and included many dependencies within R. So I decided I’d have to roll my own. Rolling my own seemed really hard, so luckily I ran into Alex Tingle’s libhex library. Though certainly not designed for hex-binning (I believe it was made with game developers in mind), this great library has all the methods necessary to create a hexagonal lattice data structure. And though written in C++, the author had completed an experimental JavaScript version.

It took some back-and-forth with libhex’s author Alex to figure it out, but the library’s methods make it easy to create a hexagonal lattice or grid of a given size with specified hexagon size. Once created, the Grid.Hex method can be used to determine corresponding hexes for each 2D point in the dataset to be binned. After this is achieved, we have a hexagonal lattice data structure, with each hex in the grid storing the points contained within its data space.

This creates the data structure, and performs the necessary binning routine for each point, but the library wasn’t meant to render anything. I therefore paired it with my favorite data-driven visualization (or document-manipulation) library, D3.js. The result is d3.hexbin.js, which can be used like so:

var hexset = d3.layout.hexbin()
    .xValue( function(d) { return d.x; } )
    .yValue( function(d) { return d.y; } )
    .hexI( hexI )
        ( data );

The result returned by d3.layout.hexbin() — hexset in the above — is simply an array of hex objects with important properties — notably data (the binned points for the particular hex) and pointString (a string representing the outline points of the hex). As far as symbolization, once the hexbinning routine is completed, representing the data with multiple symbologies is quite easy with D3. The example posted here shows off the exact same random data represented with dots, choropleth, proportional symbol, bivariate, and value-by-alpha symbologies. The code below is used to render the frequency hexgrid as a choropleth.

d3.select( "div#choroplethHexgrid" )
    .append( "svg:svg" )
    .append( "svg:g" )
        .attr( "class", cbScheme + " stroke-true" )
        .selectAll( "polygon" )
        .data( hexset )
        .enter().append( "svg:polygon" )
            .attr( "class", function(d)
            {
                return 'q'
                    + ( (numClasses-1) - scale(d.data.length))
                    + "-" + numClasses;
            })
            .attr( "points", function(d)
            {
                return d.pointString;
            });

All the code is stored in the hexbin-js Github repository. Please browse the src and tests folders to see more of what’s going on here.

Because I’m a cartographer (or something), I wanted to create a geographic proof-of-concept for this method. I came up with this, combining my custom hexbin layout class with D3.js and Polymaps. The resultant interactive visualization shows an overview + focus view of all Walmarts in the USA. Hexes can be moused over for a focus view.

d3.layout.hexbin requires D3.js, though the dependencies don’t go that deep, so a few quick mods would allow you to use the hexbinning methods with any JavaScript mapping or graphics library. Use as you will. Many thanks to both Alex Tingle and Mike Bostock for answering my questions.

Tagged , , , , , , , , , , , , , , , , , , , , , , | Comments (24) |
Apr 11 2011

Dymaxion projection in OpenLayers

The great Buckminster Fuller created a series of Dymaxion maps utilizing various forms of his patented Fuller projection in the 1940s and 50s. The most well-known, icosahedral form of the projection (above) was devised in Raleigh, North Carolina, in 1954. Fuller intended the projection to better balance shape and areal distortion, while also eschewing the north-south cultural bias he saw in common projections.

I’ve seen a few code implementations of Bucky’s design over the years, including the Perl scripts Schuyler Erle wrote for his touchstone Mapping Hacks. Erle’s modules were based on Robert Gray’s foundational work in determining the appropriate transformation equations which were then incorporated into C source code. But I hadn’t seen a client-side implementation until I saw this map in the examples section of Jeff Heer and Mike Bostock’s excellent JavaScript visualization framework Protovis. In this post I just show how their JavaScript Dymaxion code can be brought into OpenLayers as a custom projection.

Since Buckminster Fuller, Robert Gray, and Mike Bostock have already done all the hard work, adding the projection to OpenLayers is a cinch. But I think it’s worth showing here because there isn’t much info out there on using custom (that is, outside of PROJ.4) projections in OpenLayers. And I’d love to see more online slippy maps using such experimental projections.

OpenLayers implementation

Most web mapping frameworks only display data in the Web Mercator projection. This is basically because of a decision Google made six or seven years ago and because web mapping platforms have been used more for reference than thematic mapping. OpenLayers is unique in allowing coordinate system transforms from any arbitrary projection to any other. Of course, if you’re loading in Google or Bing tiles, you’ll have to stick to Web Mercator for any overlays; in this case OpenLayers will just be transforming your overlay data from lat/long to Mercator for display. But if you’re using all vector data — from KML, GeoJSON, or many other formats — you can take advantage of OpenLayers’ projection abilities. And this is almost always going to involve the Proj4js library, a port of PROJ.4.

Bjørn Sandvik provides a great introduction to projecting KML data with OpenLayers and Proj4js. Proj4js contains most of your old favorites, like Lambert and Albers and Transverse Mercator. But for custom projections like Dymaxion, OpenLayers includes the OpenLayers.Projection.addTransform method, which I’m using like so:

OpenLayers.Projection.addTransform( "EPSG:4326", "DYMAX",
    function( point )
    {
        var converted = convert_s_t_p( point.x, point.y );
        point.x = converted.x * 150;
        point.y = converted.y * 150;
        return point;
    }
);

EPSG:4326 in the above method represents the standard WGS 84 lat/long coordinate system. “DYMAX” is an arbitrary string that we’ll use whenever we want to apply the Dymaxion transformation. The convert_s_t_p method is from the dymax.js code included with Protovis and does all the heavy lifting of converting lat/long points to Fuller x-y coordinates. Notice I’m only defining the forward transformation — from lat/long to Fuller. The inverse would be quite difficult but is luckily not necessary for projecting geodata onto a Dymaxion map.

To utilize the defined projection, then, we just have to instantiate an OpenLayers.Projection object with our “DYMAX” projection identifier, and include this as an option when we create our OpenLayers map.

var map = new OpenLayers.Map("olmap", {
    projection : new OpenLayers.Projection( "DYMAX" ),
    maxExtent : new OpenLayers.Bounds( 0, 0, 860, 400 ),
    allOverlays : true
} );

Below’s an image linking to an example of the Protovis Dymaxion code being used within OpenLayers. View source on that page to see the very little code that’s driving the example. The triangles and world countries should load right away in the Fuller projection, but the 3000+ world cities may take a bit.

Next

I’d be remiss if I didn’t mention Mike Migurski’s remarkable work on the “Faumaxion” projection, which resulted in an experimental and path-breaking interactive browser that re-orients and re-configures its equilateral triangular coordinate system based on the map center and scale. Ideally something similar would be possible using OpenLayers and the icosahedral geometry of the Dymaxion projection. But that’s way ahead of me and this post. Please see Mr. Migurski’s posts (I, II, III, and IV) for more information on the Dymaxion transformation and Migurski’s reasons for switching to a gnomonic projection thanks in part to its extant and efficient inverse equation.

I just want to see more and more geographic projections available in web mapping frameworks. An argument can certainly be made that no more than a handful of projections are necessary for the vast majority of reference and thematic mapping purposes. But this leaves out certain artistic and political mapping pursuits that may benefit from more experimental projections like the Dymaxion.

Gene Keyes, a Fuller devotee, has declared a similar but earlier octahedral projection (below) by B.J.S. Cahill superior to Fuller’s (h.t. the Map Room). So next I’d like to see about implementing Cahill’s also-patented “butterfly” projection for vector data in JavaScript. Both Fuller and Cahill are in a class of interrupted projections that are 1) especially difficult to implement for vector data because of section crossings and 2) potentially quite useful for mapping global datasets due to minimized shape/area distortion and the horizontalization of the classic world map projection’s north-south orientation.

Much love to the Buckminster Fuller Institute, the current patent-holders of Fuller’s geographic transformations. And again full credit must go to the Protovis people for their client-side implementation of the Dymaxion/Fuller projection algorithm.

Tagged , , , , , , , , | Comments (9) |